Whether defining dimensions for a pipe system, specifications for pumps or heat exchangers, or generally deciding on mixing and filling process, viscosity measurements provide a wealth of valuable data to process engineers.
Contact us now for a rapid and accurate characterisation of viscosity of your samples or discuss your process challenges.

Measuring the viscosity of pastes, slurries, gels and suspensions can be a real challenge without the right equipment. The non-Newtonian behaviour of these materials presents a number of challenges to a simple viscometer:
- Multiple viscosity readings must be taken at different shear rates to characterise degree of non-Newtonian behaviour.
- Shear conditions of ‘simple’ viscometers are often undefined, and irrelevant to the processing conditions of interest.
- These materials are often in-homogeneous – large particles can interfere with reading of the true viscosity.
- Temperature can be difficult to control in large samples.
Our lab specialises in characterising the physical properties of soft materials for a number of different industries. We can ensure a high level of control over a number of measurement characteristics, including defined shear stresses, shear rates, gap sizes, deformation regimes, temperature control, solvent loss, etc. To help make use of this data we also assist in fitting models, and support every single report with a web-meeting for Q&A.
Viscosity Profiling
The viscosity of a material determines how much effort is required to move the material at a certain rate or simply put the resistance to flow. Our lab can very quickly determine viscosity across a range of shear rates and present information in a number of ways that makes it easy to quickly apply.
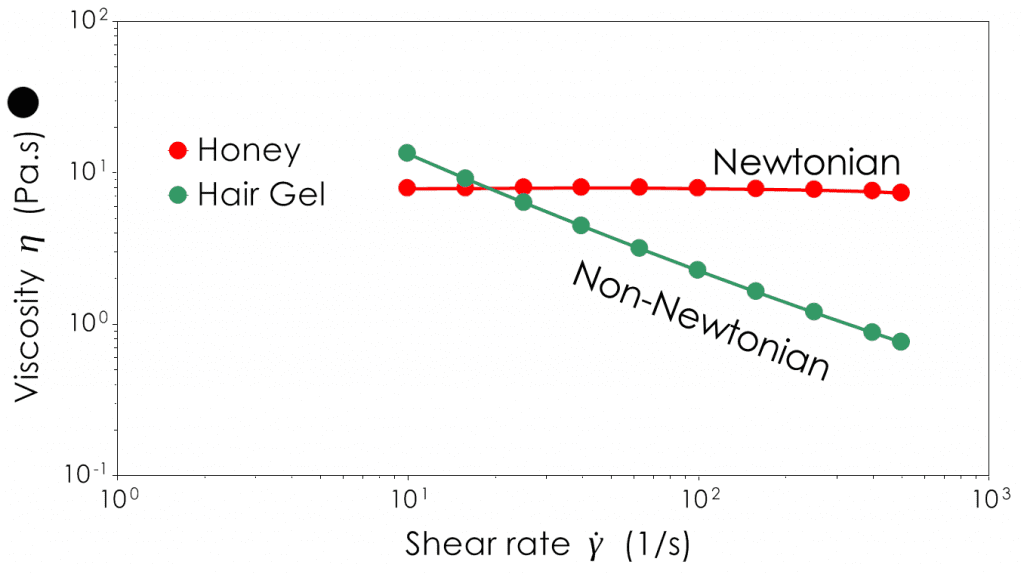 Newtonian samples do not change their viscosity based on the shear applied whereas non-Newtonian samples will decrease (shear-thin) or increase (shear thicken) their viscosity.
Newtonian samples do not change their viscosity based on the shear applied whereas non-Newtonian samples will decrease (shear-thin) or increase (shear thicken) their viscosity.
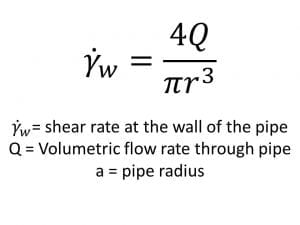
Shear rate is often a necessary metric for pipe flow calculations. To calculate the shear rate experienced by a material flowing through a cross section of pipe we can use the following equation.
However, shear-thinning materials are better described by the following equation.
The power law index is a constant generated from a model fit to experimental data, and helps to describe the “non-Newtonianess” of a liquid.
Power Law Equation
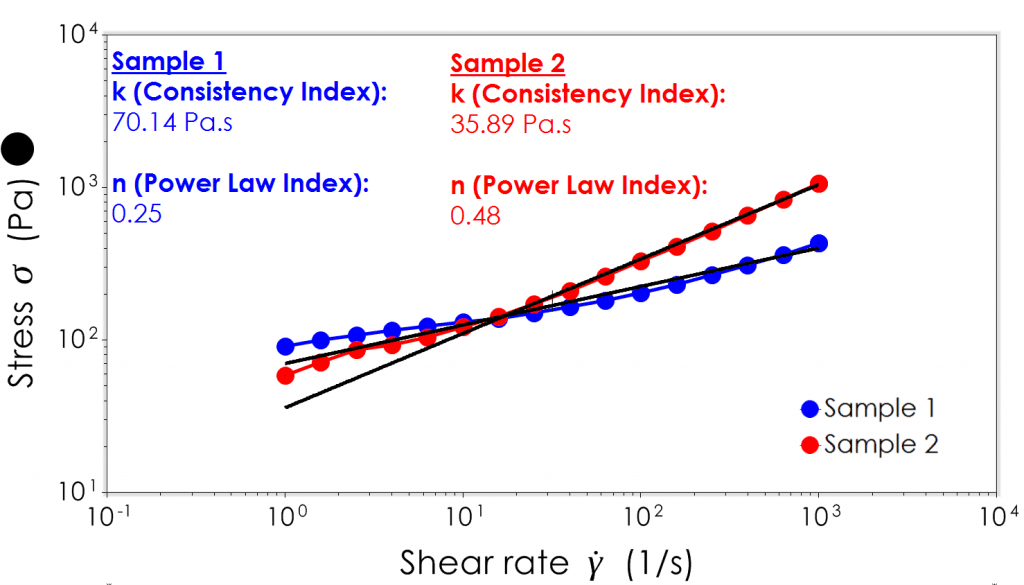
 The power law equation is a simple and practical equation for describing shear stress-shear rate relationships across a range of shear rates common in processing.
The power law equation is a simple and practical equation for describing shear stress-shear rate relationships across a range of shear rates common in processing.
The power law index of a material is an indicator of its Newtonian behaviour; a value of 1 is a perfect Newtonian material, <1 is indicative of shear thinning behaviour and >1 is indicative of shear thickening behaviour.
The “consistency index” can be thought simply as a constant that determines the relative position on the stress axis of a shear stress-shear rate curve at low(-ish) shear rates. The higher this value, the higher the location of the curve and generally more effort will be required to pump this material.
In the graph above, we’ve applied a power law model fit to some real world data. The crossover point for both data sets is within the typical measurement region of a Brookfield Viscometer, highlighting the importance of taking a full flow curve for a sample. Beyond shear rates of 1,000s-1, sample 2 requires more than twice the effort to pump when compared to sample 1.
The model fit has quite a large deviation at lower ends of shear rate suggesting that these materials have more complex behaviour that can’t be adequately described by just a power law relationship and indeed this model does not take into account the effort required to get the material moving in the first place.
Herschel Bulkley Equation
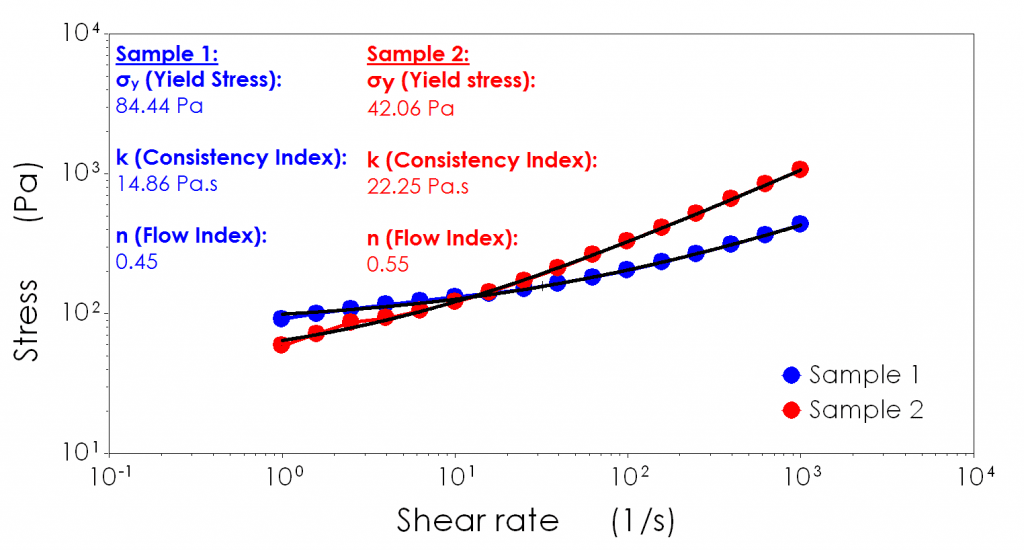
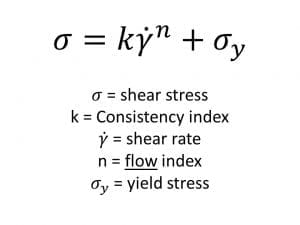 The Herschel Bulkley equation, is similar to the power law equation however, attempts to address materials which have a “yield stress”. A yield stress is a common feature of structured liquids which display solid-like/elastic behaviour under low stress conditions. Typical examples can include mayonnaise, ointments or gels.
The Herschel Bulkley equation, is similar to the power law equation however, attempts to address materials which have a “yield stress”. A yield stress is a common feature of structured liquids which display solid-like/elastic behaviour under low stress conditions. Typical examples can include mayonnaise, ointments or gels.
The simplest way to think of yield stress is how hard a material needs to be pushed until it switches from solid-like (elastic) behaviour to liquid-like (inelastic/plastic) flow behaviour. It is a useful metric for determining initial pump start up conditions and can explain why some materials can have a low viscosity but are a pain to pump from “cold”.
In this instance, the Herschel-Bulkley model has provided an improved fit to the data. It’s important to realise the “k” and “n” values for both the power law equation and Herschel Bulkley equation are not interchangeable.
Viscosity Temperature Relationships
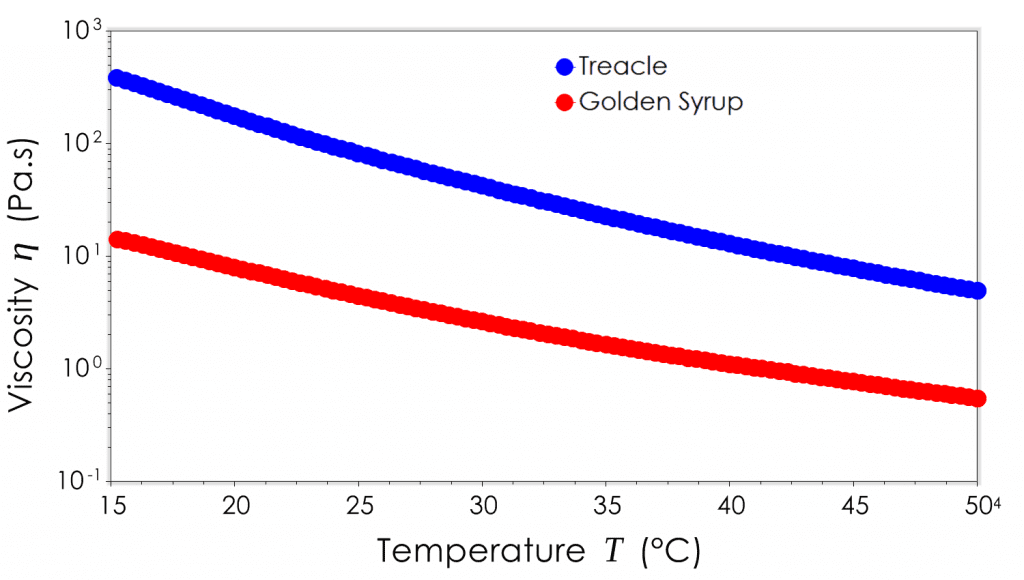
Temperature can have a number of effects on the physico-chemical properties on a material, and is often one of the easier process parameters to control. Generally an increase in temperature decreases fluid viscosity. For Newtonian materials we can directly measure this relationship by looking at viscosity at a single shear rate as a function of changing temperature. This relationship isn’t always necessarily linear as we have shown in the graphic below.
For non-Newtonian materials, the overall viscosity, degree of shear thinning and in some cases the yield stress can be affected to varying degrees by changes in temperature. In this instance it is best to look at a full flow curve at specific temperatures within the range of interest.